

Irreducibility and periodicity both concern the locations a Markov chain could be at some later point in time, given where it started. A Markov chain is ergodic if all its states are. A state is known as ergodic if it is positive recurrent and aperiodic.A recurrent state is known as positive recurrent if it is expected to return within a finite number of steps, and null recurrent otherwise. A state is known as recurrent or transient depending upon whether or not the Markov chain will eventually return to it.Absorbing states are crucial for the discussion of absorbing Markov chains. An absorbing state i is a state for which Pi,i = 1.A Markov chain is known as irreducible if there exists a chain of steps between any two states that has positive probability.If all states are aperiodic, then the Markov chain is known as aperiodic. If k = 1, then the state is known as aperiodic, and if k > 1, the state is known as periodic. A state i has period k ≥ 1 if any chain starting at and returning to state i with positive probability must take a number of steps divisible by k.Let PP be the transition matrix of Markov chain. What are the properties of a Markov chain?Ī variety of descriptions of either a specific state in a Markov chain or the entire Markov chain allow for better understanding of the Markov chain's behavior. This means that means that the transition probabilities matrix Pi, j (n, n + 1) is independent of n. An infinite-state Markov chain does not need to be steady state, but a steady-state Markov chain has to be time-homogenous. This phenomenon is referred to as a steady-state Markov chain. It is possible for a Markov chain to be stationary and therefore be independent of the initial state in the process. Continuous-time: Any continuous stochastic process with the Markov property (for example, the Wiener process).Discrete-time: Markov chain on a measurable state space (for example, Harris chain).Continuous-time: Markov process or Markov jump process.Discrete-time: Markov chain on a countable or finite state space.The system's state space and time parameter index need to be specified. This means that we have one situation in which the changes happen at specific states and one in which the changes are continuous.

These are: discrete-time Markov chains and continuous-time Markov chains. While it is possible to discuss Markov chains with any size of state space, the initial theory and most applications are focused on cases with a finite (or countably infinite) number of states. They arise broadly in statistical and information-theoretical contexts and are widely employed in economics, game theory, queueing (communication) theory, genetics, and finance. Markov chains may be modeled by finite state machines, and random walks provide a prolific example of their usefulness in mathematics. This simplicity makes it possible to greatly reduce the number of parameters when you are studying such a process. To simplify this, lets just say that this means that when you know the current state of the process, you do not require any additional information of its past states in order to make the best possible prediction of its future. This means that the past and future are independent when the present is known. They are utilized to a great extent in a wide range of disciplines.Įssentially, a Markov chain is a stochastic process that satisfies the Markov property. These Markov chains are a fundamental part of stochastic processes. The state space, or set of all possible states, can be anything: letters, numbers, weather conditions, baseball scores, or stock performances. In other words, the probability of transitioning to any particular state is dependent solely on the current state and time elapsed. The defining characteristic of what a Markov chain is that, no matter how the process arrived at its present state, the possible future states are fixed.
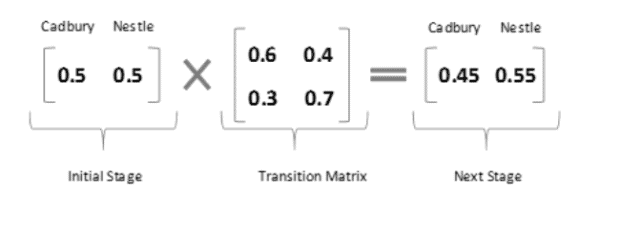
A Markov chain is a mathematical system that experiences transitions from one state to another according to certain probabilistic rules.


 0 kommentar(er)
0 kommentar(er)
